今月から新3年生としてのマンスリー講座が始まりました。
3年生ということで、早速図形の問題が入ってきています。
まずは
色塗りされた図形の広さは、何マス分ですか?
といった問題です。
たとえば以下のような図形が与えられます。
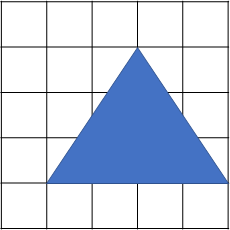
これらは図形の面積を求める基本で、様々な参考書でも定番の内容です。
基本問題はちょうどマス目の半分の三角形などがあり、
うまく正方形のマス目を作っていくようなものです。
その後、少しずつ難しくなって上図のような
複数のマス目を組み合わせた長方形を考え、長方形のマス目の半分を求める
という考え方を導入していきます。これは三角形の面積の求め方を自然に理解させるためで、
長方形の横の長さを底辺、縦の長さを高さとしてマス目の数をかけ算し、
半分の広さだから求めた長方形のマス目の広さの半分が塗られた部分の面積となる
という問題です。上図でいえば三角形をまるごと1個で考えるのではなく、
三角形を左右に二等分してふたつの直角三角形として考え、
直角三角形は横2マス、縦3マスの長方形の半分だから2x3÷2=3マス分
として求め、
それが2つあるから全部で6マス分の面積
という感じで計算していきます。パズル的要素と計算を組み合わせた楽しい問題です。
娘はパズル道場で学習していたので、どのような形も簡単に計算できたようです。
状況によっては
全体のマス目(上図の例題なら5x5=25のマス目)から、
塗られていない部分の面積を求めて25から引く
といったやり方の方が早いこともあります。
この辺の思考の柔軟性は普通にできるようになってほしいという感じでした。
次回はパズル的要素の応用として、
指定されたマス目の広さの正方形の作り方
に触れたいと思います👋