まだまだ続く11月マンスリー講座・・・😓
いよいよ「数の性質と条件整理の複合問題」の最後の回です。
しかし11月のマンスリー全体でいうと
やっと半分が終わった😱
というえげつなさです。お、重い・・・😬
前回の記事「その3の2:マンスリー講座11月」はこちら
girl.chugakujuken-challenge.work
「数の性質と条件整理の複合問題」ですが、最後は等差数列を考える問題でした。
順に説明します。(1)は簡単です。

タテとヨコは等差数列になっています。Aを求めなさい、ということです。12と17から、
ヨコは差分5の等差数列となります。したがってタテヨコの交差マスは27です。
するとタテは差分3の等差数列になりますから、Aは24-6=18と求められます。

こちらはBを求めます。ひねってあるのは、左上で25と17が1マス開けてあることです。
差が2個分になるので、等差は(25-17)÷2=4となります。17の右隣は13ですね。
次にタテの列の13と25の関係も同様に(25-13)÷2=6、
タテ列の25の下は31になるので、下段のヨコ列は(49-31)÷2=9となり、
差分9の等差数列になります。したがって、さっき求めた31のマスから左に一つ分で、
31-9=22がBの答えとなります。
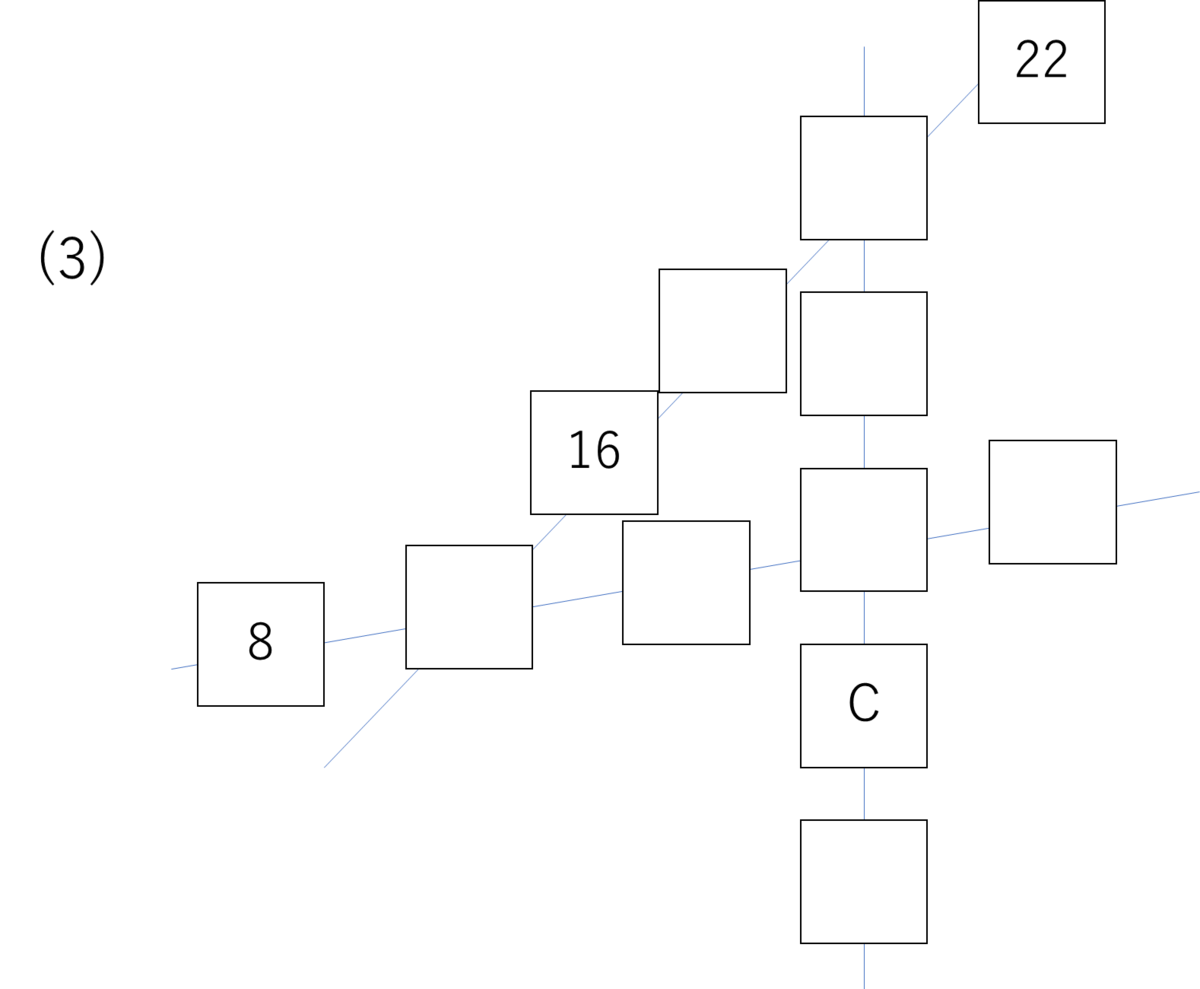
まずは(22-16)÷3=2で、ナナメの等差数列を出します。
16から22までの差(マスとマスの隙間)は3個なので、3で割ったよ~
ということですね。
すると16の左下が14になるので、ヨコは差分6の等差数列になります。
22の左下のマスが22-2=20。ヨコの列の右から2番目のマスが、
14+6+6=26となります。この20のマスと26のマスは2つ離れているので、
(26-20)÷2=3で、タテは差分3の等差数列です。したがってCのマスは
26+3=29となります。

エッ、エッグ~い😱
と私は思いました。2年生でか・・・と。これ相当な仮説思考力が必要なんじゃないか?と。
どこから手をつければいいか🥴悩むので、まずはマス目に名前をつけましょう😅
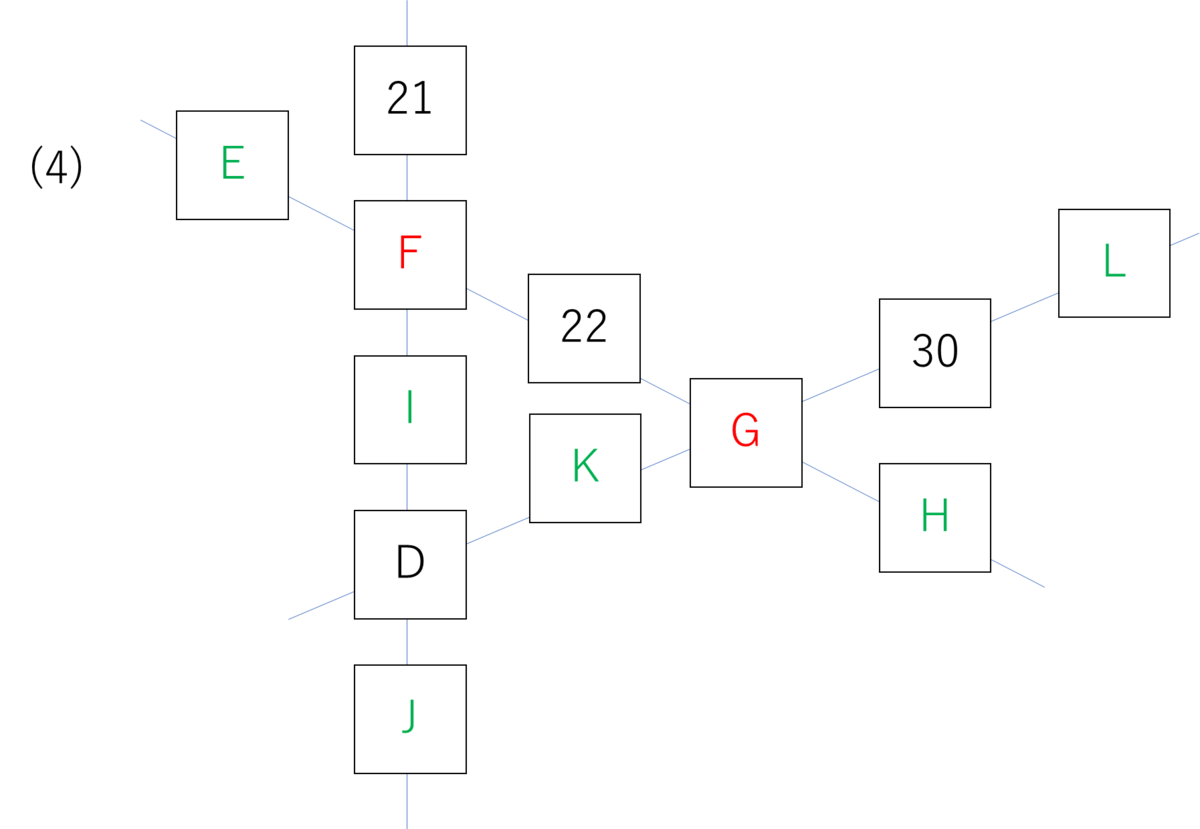
初見は自力で解きましたが、この問題は解答に解説がついていました。助かった・・・
鮮やかです。言われてみれば
ああ、そうだよ。数列の性質をちゃんと使ってる
とわかります😓でも解説見るまで気づかなかったかな・・・🥴
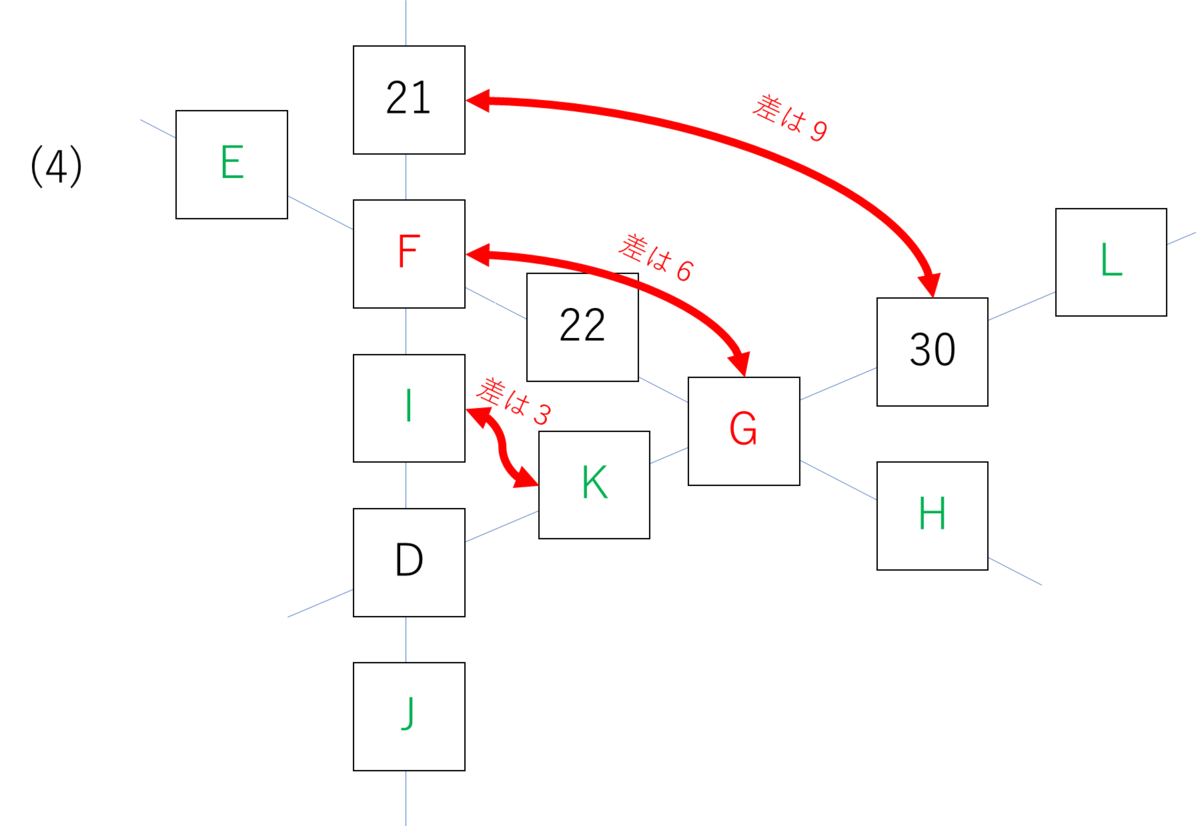
まずDから見て、21も30も「それぞれの列で3つ離れたところにある」がポイントです。
Dから3つ離れた時、30と21は差が9になっています。つまり
Dからひとつ離れるごとに、タテとナナメの数字は3ずつ差が開く関係である
ということです。30-21=9です。そしてDからは3つ離れていますから、
ひとつ離れると開く差が、9÷3=3であるという意味です。
すると30と21の一つ前のマスであるFとGは差が6ですから、
F=19・G=25かF=25・G=19ですが、F>GとするとDの数字がおかしくなるので、
F=19とG=25しかありえません。
このままだと難しいので、以下のような説明を追加したらいいかな?と思いました。
21を含む数列はD,I,F,21です。差分をXとします。
30を含む数列はD,K,G,30です。差分をYとします。
これは以下のように見なせます(この後の説明のため、数列を上下入れ替えます)。
「2つの数列で見比べる」
D,(D+Y),(D+Y+Y),(D+Y+Y+Y)←30
D,(D+X),(D+X+X),(D+X+X+X)←21
同じ「D」という数から始まりますが、差分がXとYで異なるため、少しずつ差が開いていきます。
上の列から下の列をそれぞれ引いてみると、
ひとつめの差はD-D=0
ふたつめの差は(D+Y)-(D+X)=Y-X
みっつめの差は(D+Y+Y)-(D+X+X)=2x(YーX)・・・条件P
よっつめの差は(D+Y+Y+Y)-(D+X+X+X)=3x(Y-X)
この「よっつめの差」が30-21=9なので、3x(Y-X)=3、よってY-X=3
ということがわかります。
これだけだと解けないのですが、3つめの数字の関係が
図のF=(D+X+X)、G=(D+Y+Y)で、条件PよりG-F=6。
さらに等差数列でF→22→Gですから、(G-F)÷2=3が等差、F=19、G=25
が導かれます。
娘にどう教えたらいいか、これは完全に理解できなくても「面白い~」と思えればいいかな、
と思いますが、ポイントは上の「2つの数列を見比べる」で示した部分かと思います。
ちなみに私は別の、もっと非効率な解き方をしました(以下の通り😭かっこわる~😭)
まずFとGに22は入りません(等差数列なので)。次に手を動かすしかないのでFに23を入れます。
タテが差分2の等差数列、Eを含むナナメの列は差分1の等差数列になりますから、
G=21となります。するとLを含むナナメの列は差分9の等差数列になるので、
L=39、K=12,D=3と減っていきます。
一方でタテの列は下に行くほど増える数列でD=27になりますから、
先ほどのD=3と矛盾してしまいます。つまり、
タテが下に行くほど増える列だと、Lを含むナナメの列は左下に向かって減るので、
Dの数字は何も入れられなくなる
とわかります(FとGが22をはさんで大小となるので、Fが21や22より大きくなると、
Dに入る数字はなくなるということです)。
このことから、
Fは20以下の数字である
と考えられます。タテの列もLを含むナナメの列も、下に向かって減っていく列となります。
あとは、数字を入れてみます😅
タテの列の差分を2とすると、D=21-2-2ー2で15です。
このときF=19なので、G=25になります。30-25=5でナナメの等差を求めると、
D=30-5-5ー5で15となります😮
本当にこれで終わりか?ということで、タテの差分を3とすると・・・
タテよりD=21-3-3ー3で12。F=18、G=26
ナナメよりD=30ー4-4ー4で18。合わないです😌
しかもDはタテから導くとさっきより減り、ナナメから導くとDはさっきより増えました。
これはF←22←Gの等差数列から、
Fが小さくなるほどGが大きくなり、タテの差分が大きくなるのにナナメの差分は小さくなる
という関係を示しています。つまり、
これ以上タテの差分を大きくしてDを求めることには、意味がない
と判断できます。まとめると、
タテの列もナナメの列も、下に向かって減っていく等差数列であると判断する
仮の数字を入れて確かめる
と解きました。四谷大塚の鮮やかさと比べると、格好悪いですね~😵
これがテストだったら、解けたとしても間に合わない、ということです。
この問題は授業でまったく触れられなかったそうなので、教えるべき問題なのかわかりません😓
ただ、
マンスリー講座の問題難易度に上限はないのかも~😵
という絶句感はありました😅
たった2時間で、いったいどれくらいの難問をやれると想定しているのか・・・🤔
教材の半分も進めないのに、授業でポカンとしてしまった子が結構居たそうです。
マンスリー基準をクリアした子だけの集まりのはずなのに・・・😱
こんななのに、まだ「その4:マンスリー講座2年生11月」に続きます・・・👋