長々と書いてきたマンスリー講座11月。今回は最終回「規則性(等差数列ではない数列)」です。
前回の記事「その5:マンスリー講座11月」はこちら
girl.chugakujuken-challenge.work
問題は平成25年、27年・大宮開成中のものでした。
次の□に入る数を答えましょう。
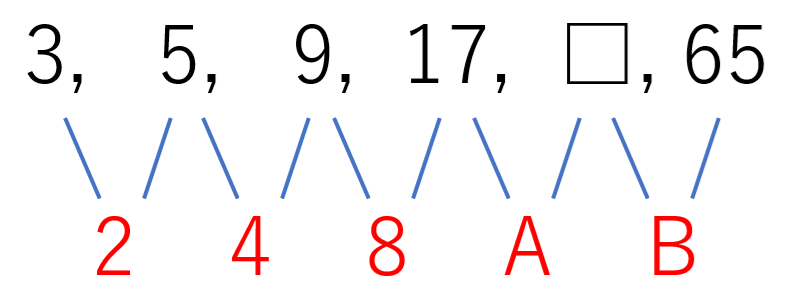
(1)3, 5, 9, 17, □, 65, ・・・
(2)3, 12, 27, 48, □, 108, ・・・
数列なので、まずは差分の確認ですね。(1)なら、差分は
5-3 = 2
9-5 = 4
17-9 = 8
□-17 = A
65-□ = B
となります。差分が2, 4, 8と増えているので、何となく「差が倍になっていく」とわかります。
べき乗という概念がなくても、上記のように視覚化すれば何かが見えそうです。そうすると
A=16かな?🤔
B=32かな?🤔
と考えることができます(手が動きます)。もしAが16なら□は33、Bが32でも□は33です。
数列のままで
と書いていっても良いです。(1)はそんなに引っ掛からないかもしれません。
(2)の差分は
12-3 = 9
27-12 = 15
48-27 = 21
□-48 = A
108-□ = B
となっていて、少しわかりづらいですね。差分が9, 15, 21なので、これを新たな数列と見れば、
差分6で9から始まる等差数列
とみなすことができます。そうするとA=27、B=33が導けます。試しにここから□を導けば、
□ = 75
となります。75-48=27ですし、108-75=33ですから、□=75は正しいことがわかります。
マンスリー講座11月最後の問題としては、
おや?🤔
と思わされる難易度です。が、子どもには難しいのかもしれません。
現に娘も、
等差数列だと思って解いたら引っ掛かった😢
という問題がありましたし。
girl.chugakujuken-challenge.work
マンスリー講座担当の先生が、
この子はパターンで解いているのか、それとも数の性質に意識が向いているか🤔
を確認するための問題なのかもしれません。
難問を楽しく解けるのがマンスリー講座の醍醐味だと思っていますが、
解き方・解き筋を身につけて、
自分の力で解いてみたい!👧😤
と思えるように、導きたいと思います。
これでやっと11月の復習は終わりですが、すぐに12月🎄⛄です😓
あと2回。どんな問題が出てくるのか、気を引き締めて待ちたいと思います💪