昨日は四谷大塚主催の全国統一小学生テストでした。
偏差値次第ですが、基準を満たさなかった場合はマンスリー講座とお別れです👋🥺
面白い問題を2年生でもわかるように教えてくれる楽しい講座なので、
できれば生き残ってほしいなと思います。今回生き残れば3年生までは通えるので・・・😅
気になる手応えは・・・
国語も算数もきっと満点💯🤩
とのこと😉
はい、でました~🤣
さて、お迎え終わった帰り道、早速採点してみました~
算数は・・・満点はなかったです。満点どころか
マンスリー大丈夫だろうか😱
という結果でした。まぁドンマイ!ですけどね😉ご愛敬。
内容としては、
ちょっと難しいかな?🤔
と思った大問6を完答できていました🤩おお~
マンスリーで一緒のお友達も受けてたそうですが、
大問7は全部できなかった😭時間足りなかった~
とのこと。娘は、
大問7の(1)、(2)の①と(2)の②の3つをすべて答えたけど(1)のみ正解
でした。大問6までにやらかしまくったので🤣、総得点は上がりませんが😖
大問7はやっぱり条件整理だったので、問題をよく読んで考えれば解けたかな~?🤔
今回は
絶対に最後は条件整理だから、よく問題用紙を汚してこいよ~👋
と送り出したのですが、問題の読解力が足りませんでした。
条件を一つ見落としてしまいましたね😅これは仕方ない、難しかったね、と。
(2)の①が解けないと②は解けなくなっているので、この2問はセットで10点です。
自宅に帰って解説をしました。
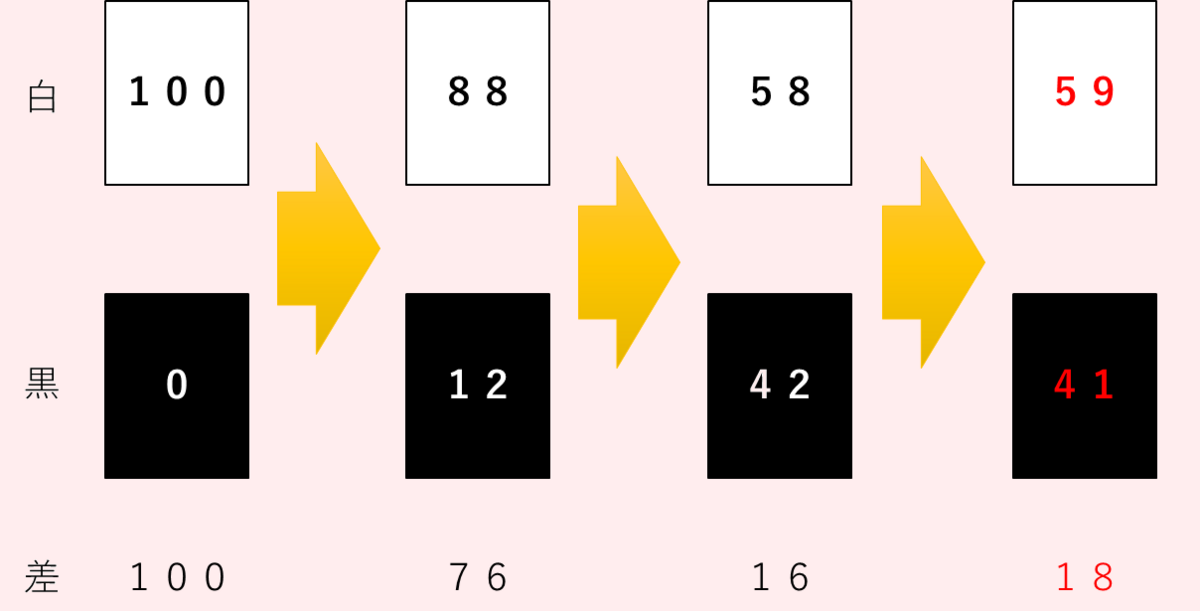
片面が白、反対面が黒のカードが100枚あって、2人の子どもがそれぞれひっくり返した
という問題です。
最初に100枚すべて、白が見えている状態からスタートします。
男の子が12枚ひっくり返したあと、女の子が”白と黒のカードを合わせて30枚”
ひっくり返したところ、白が黒より32枚多くなりました
という条件です。とりあえず解き方を2通り示します。
※この問題には説明の不足を感じます。というのも
”男の子が全部「白→黒」にしたかはわからない”
を疑問に思うかもしれないのです。男の子が最初に6枚「白→黒」したあとに、
”同じカード”を6枚「黒→白」にすると、白100枚に戻せてしまいます。
ここに引っ掛かると(2)の②がうまく解けません。私としては問題文に
「ただし、男の子はすべて別のカードをひっくり返しました」
みたいな補足を書いてほしかったです。厳密には”のべ12枚”と書かれていないし、
女の子の説明だけ「女の子は白と黒のカードを合わせて30枚ひっくり返した」
と書かれているので、男の子は「白→黒」しかしなかったように解釈はできます。
しかし男の子が「黒→白」も行ったとすると②の答えが5通りできてしまうので、
補足した方が良いと思いました。この不足は「それも含めて注意力を要する読解力」
といえるような難化手法になってはいないと思います。
まずは”楽になるけど2年生ではなく3年生の解き方”です。3年生ならすぐ解けます。
線分図です(和差算の基本)。配られた四谷大塚の解説は線分図でした😬
SAPIXではまだのはずですが、リトルスクールではもうやってるの??😮
3年生のはずだと思ったけど・・・?
(A:線分図方式)
こうすると、白は黒+32だとすぐわかります。そして白と黒の合計は100なので、
白+黒=100と、黒+32=白の2つから、(黒+32)+黒=100が導けます。
もう簡単。100-32=68で、これが黒+黒なので、黒が34枚。白は66枚です。
3年生だと大問2くらいで出てくるレベルでしょう。
(B:地道に計算。つるかめ算方式)
※娘には最初こちらで教えてから、線分図も教えました。線分図がわかれば一瞬だよ!と
まず男の子が12枚「白→黒」でひっくり返したとすると、白88枚・黒12枚です。
ここから女の子が「白→黒」と「黒→白」を合わせて30回ひっくりかえしています。
もし88枚の白を30枚「白→黒」すると、白58枚・黒42枚で差が16枚です。
※娘には以下のように図で示しながら説明しました。
差が小さすぎるので「30枚全部が”白→黒”ではない」と考えます。なので黒を減らしていきます。
黒が1枚減ると白が1枚増えるので差は2広がります。この差が32になればいいので、
白58・黒42・差16から差が32になるまで、あと16だけ差を広げるということです。
黒を1枚減らせば差が2広がるので、16の差を広げるには黒を8枚(16÷2)だけ
減らせばいいことになります。したがって、42ー8で黒が34枚。白は66枚になります。
次の問題(2)の②は
では、女の子がひっくり返した30枚のカードのうち、白から黒にひっくり返したカードと、
黒から白にひっくり返したカードはそれぞれ何枚ですか?
というものでした😮さすが四谷大塚。最後はややこしいものを入れてきますね~😅
ちなみに私のブログでは図を描いていますが、本番の問題に図はありません!ひえ~😱
でも解ける子は解けるでしょうね。図を描ける子、あるいは3年生まで先取りしている子・・・。
男の子は「12枚すべてを白から黒にひっくり返した」という前提で進めます。
基本的にはつるかめ算みたいな発想で解けばいいかな?🤔と思います。
下の図の真ん中の状態から”30枚ひっくり返して”、右端の最終形にすることになります。
まずは真ん中の状態から30枚、全部「白→黒」にしてしまいましょう😅
すると白58・黒42の、①の解説で出た状態になります。これがあるので、線分図より
つるかめ算で解いていた方が、②を完答できる可能性は高まるかな~と思いました。
※試験時間がない時は「①を線分図で秒殺して②は捨て」で得点を稼ぐかもしれませんが😉
白88からの最終形は白66なので、白は22枚ひっくり返せばいいはずです。
でも女の子は30枚ひっくり返していますから、あと8枚余計にひっくり返す必要があります。
1枚「白→黒」でひっくり返したら、それを打ち消すために1枚「黒→白」をしなければ、
白66・黒34の状態を維持できません。つまり
1枚「白→黒」をしたら1枚「黒→白」をすればいいので
4枚「白→黒」をやって、4枚「黒→白」をすればいい(合計8枚分)
ということになります。すると最初に22枚「白→黒」をひっくり返していますから、
あと4枚分の「白→黒」と4枚分の「黒→白」と合わせて
「白→黒」が22+4=26枚
「黒→白」が4枚
ということになります😉
ちなみにここで「男の子も白→黒、黒→白の合計で12枚をひっくり返した」となると、
正解が5通りになって非常に困ります😠
例えば男の子が8枚「白→黒」4枚「黒→白」だと、女の子は「白→黒」30枚です。
同様に、
男の子が「白→黒」9・「黒→白」3なら、女の子は「白→黒」29・「黒→白」1
男の子が「白→黒」10・「黒→白」2なら、女の子は「白→黒」28・「黒→白」2
男の子が「白→黒」11・「黒→白」1なら、女の子は「白→黒」27・「黒→白」3
となるので、正解となっている
男の子が「白→黒」12・「黒→白」0なら、女の子は「白→黒」26・「黒→白」4
と合わせて5通りになります。
これが大問7でしたが、①が解ければ②も解けるかも🤔という感じでした。
個人的には図形問題っぽい大問6の方が難しく感じましたが、どうでしょう?
図形と条件整理を組み合わせた大問6
和差算と条件整理を組み合わせた大問7
どちらも得点の分かれ目だったのではないかな?と思います。
娘は大問6が短時間で解けたおかげで、大問7の(1)が無事に解けました。
マンスリーのお友達は大問6でつまずいたのかもしれません。授業の様子を聞く限り、
恐らくそのお友達は大問7が解ける力を持っています。大問6と7が逆の順序だったら、
娘はさらに10点落としていたかもしれない、ということです🥶
そういう意味では、やらかしたけど少し救われた今回の算数😐
平均点と点数分布は、どうなりますでしょうか~・・・😅