「マンスリー」講座というだけあって、1か月を飽きさせずに過ごせるボリューム😓
の、マンスリー11月です😭
今回は5つ目の「和差算」です。あと2回だ!
前回の記事「その4:マンスリー講座11月」はこちら
girl.chugakujuken-challenge.work
11月は
数の性質(9月から続く、平均に関連したもの。但し応用がきつい😓)
条件整理・推理
数の性質と条件整理の複合問題
距離の比較(和差算そして線分図への導入)
和差算
規則性(等差数列ではない数列)
でした。あと2回、今回の和差算をやったら、あとは規則性だけ・・・。
和差算は、平成26年・東京家政学院中の問題を少し改版したものでした。
りんご1こ、みかん1こ、もも2こを買うと530円で、
りんご1こ、もも1こを買うと310円になり、
りんご1こ、みかん1こを買うと150円になります。
りんご、みかん、ももの1このねだんはそれぞれ何円ですか?
大人だったら連立方程式の代入法をサクッと使いますかね~?😅
(りんご1+みかん1)=150円
(りんご1+みかん1)+もも2=530円
ですもんね。一瞬で桃が出ます。そうするとリンゴも出ますので、みかんも出ます。
みかん🍊安すぎるだろっ!🍎と🍑が高いぞ!
と言いたくなりそうです。
さて解ければいいというわけではないですし、この問題の前(前回の記事)は
距離の比較(和差算そして線分図への導入)
ですから、
線分図という武器に慣れてみよう!入試問題を解いちゃおう!
という四谷大塚の意図を感じます。
作るべき線分図は以下のような感じでしょうか。
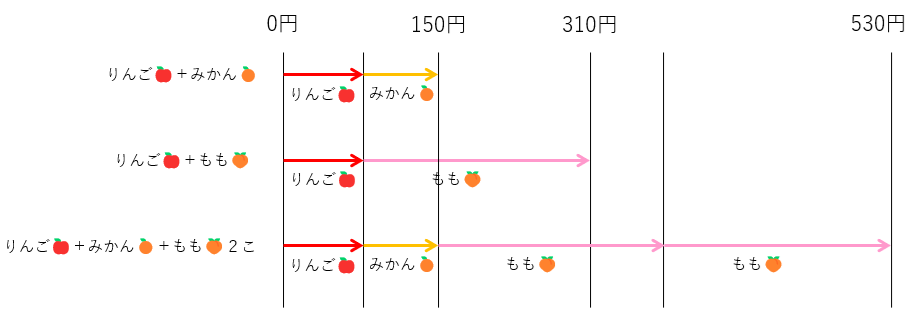
1個の正確な値段がわからないので、縮尺は最初、いびつなものになります👍
但し”使える線分図”を描くためのポイントはあると思います(以下)。
- 同じ要素をなるべく左にそろえる(最初に使う)→今回なら共通要素である”りんご🍎”
- 合計の小さいもの、または問題によっては大きいものを最初に描く(図の基準サイズ)
特に1は大事です。線分(列)ごとに要素がバラバラだったら、比較ができません。
たとえば、1列目は左端がみかん、2列目は左端がりんご、となっていたら、
1列目のみかんと2列目のももを比べにくくなります。娘には
基準、比べるもののスタート地点を揃えようね~😉
と教えます。まずは線分図を自在に描けるようになってほしいと思います。
上の図なら、1列目と2列目を比べると、みかんとももの値段の差は160円だとわかります。
1列目と3列目を比べれば、もも2個の値段が「530-150=380円」とわかります。
このことから、もも1個が190円だとわかれば図に書き込んでいき、
2列目からりんご1個が120円、1列目から150-120でみかんが30円とわかります。
線分図を描くのは手間ではあるのですが、
視覚化してすべての情報が正しく整理されていること
が確実になれば、見直しの時間を短縮できます。つまり、トータルで見れば早く解き終わります。
落ち着いて確実に解ききることは、見直しの効率化にも寄与しているということです。
速く解いて見直しの時間をたっぷり取る=もう一度解き直す、ではなく、
見直しは「解き直しでなく、解き筋の確実性を確認する」
ということだと私は思います。そうすれば、もう一度解く必要はありません。
答えの見直しではなく解き筋の見直しこそが、真の意味での見直しだと思います。
計算問題でも、暗算で解いて見直しでもう一度解くよりも、
最初に筆算で計算過程を残しておき、見直しでは筆算の式を見て
繰り上がり・繰り下がりを忘れていないか
数字を間違えていないか
を見た方が、間違いを発見しやすくなります。
暗算で2回解いて答えが違っていたら、自動的に3回目の計算が待っています。
これは時間がかかりますし、1回と2回なら2回同じになった答えの方が正しそうに見えても、
2回間違えている可能性はゼロではありません。
それならば、計算過程を残しておいてプロセスを確認した方が効率的だと思います。
だからこそ、塾の先生は
ミスではなく実力ですよ~(プロセス=技術が確立されていませんよ~)
というのだと思います。
このような意図があるので、娘には線分図も含めて
視覚化の重要性と、正しいプロセスの反復
を丁寧に伝え、低学年の、易しい問題のうちに技術を身につけさせたいと思います。