4月のマンスリー講座は、あと「2.図形の分割」以外に
中学入試問題にチャレンジ!
を残すのみとなりました。前回の記事はこちら
girl.chugakujuken-challenge.work
中学入試問題まで記事にするかどうかは、これから考えます😓(問題自体は数の性質)
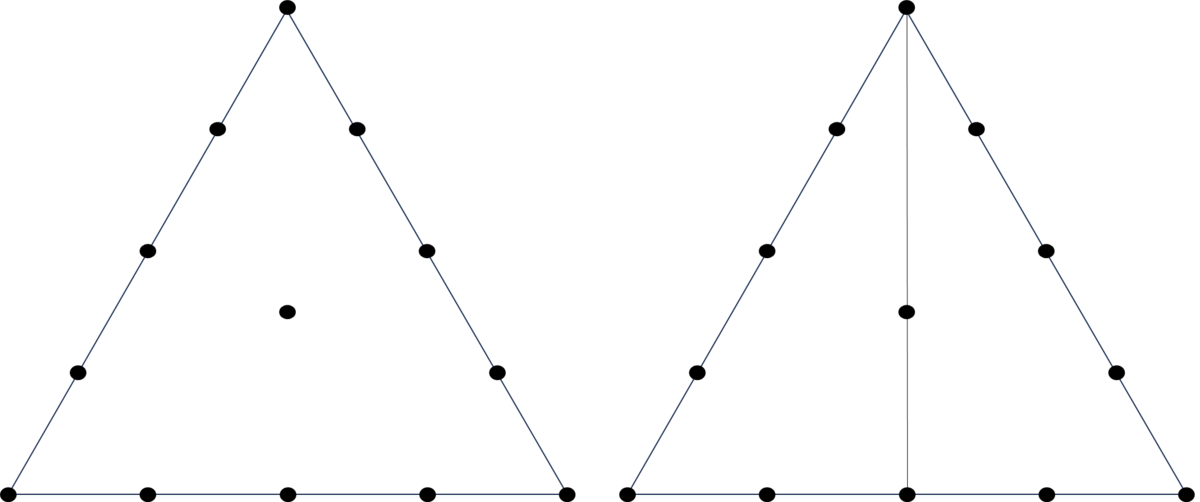
さて「2.図形の分割」の最後の問題は、正三角形の分割でした。まずは説明文👆
下の図では、正三角形の真ん中に点をうっています。また、各辺に等間隔の点をうっています。
これらの点を利用して、正三角形を同じ広さになるように分けます。
下の図で右の例は、正三角形を2等分したものです。
(問1)正三角形を3等分する分け方を考えましょう
(問1の解答例)
左の図はいかにもという感じですが、右はどうでしょう?
- 点を利用すること
- 広さが等しくなるように分けること
という条件は満たしています😅
複数の分け方が考えられる場合は、すべて書きなさい
と言われることもあると思うので、いろいろ試していいんじゃないかなと思います。
次は少し難しくなって
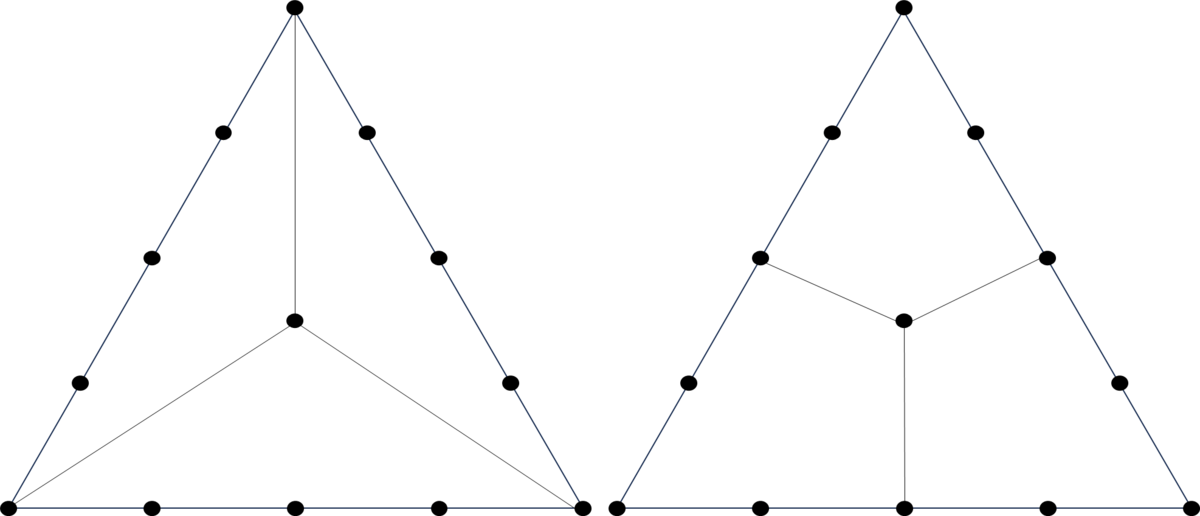
(問2)正三角形を8等分する分け方を考えましょう
です😅
(問2の解答例)
どうでしょう。8等分というのがいやらしいなぁと思いました🥴さすがマンスリー講座😁
等間隔の中間点が各辺に3個ずつなので、3等分や6等分、12等分など
3の倍数となる等分だったら考えやすいのになぁ
と思いました。8等分に至る考え方としては
いきなり8等分は難しいので、まず4等分できる方法を考えよう
4等分できたら、それを半分にできればうまくいきそうだぞ
という感じだと思います。図形の分割といいながら、倍数の概念がちゃっかり入ってます😅
平面図形といえど算数ではあるので、数の概念を用いるのも面白いかなと思います。
最後の問題はこんな感じでした👇
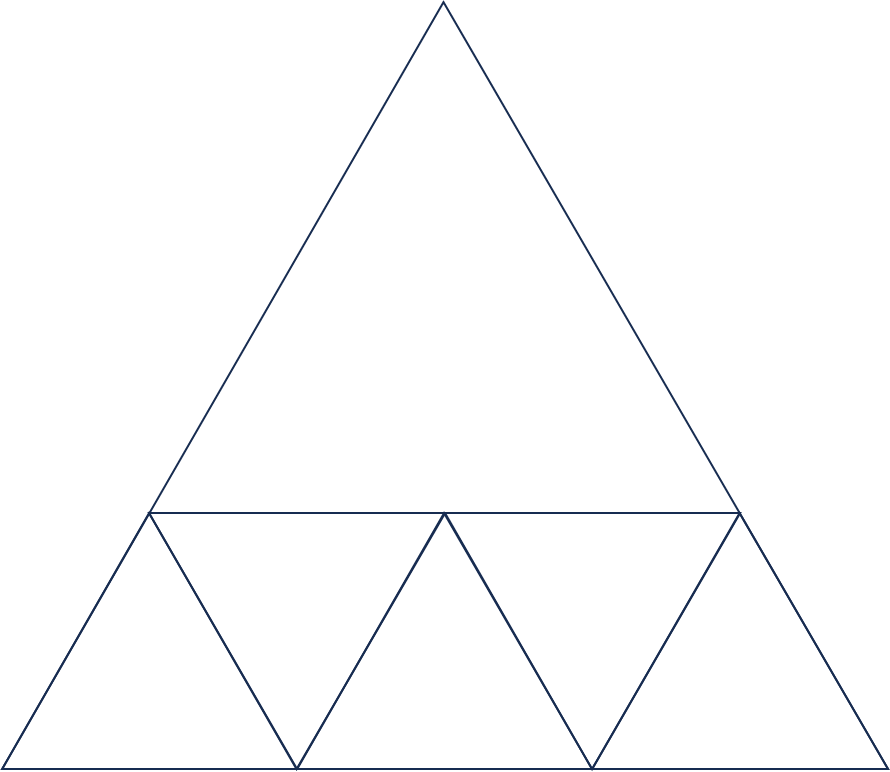
下の図の左のような正三角形の中に直線を引いて、いくつかの正三角形に分けます。
右のように直線を引くと8つの正三角形に分けることができます。
これについて問いに答えましょう。
今度は広さしばりでなく、正三角形しばりですね😅
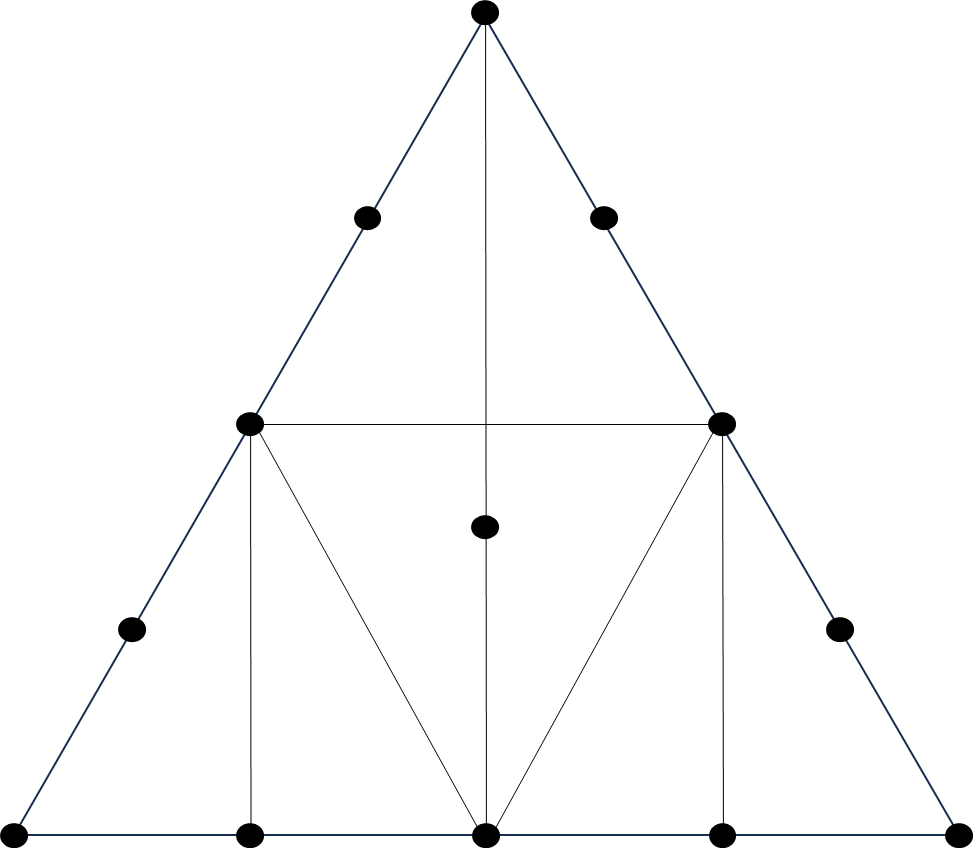
(問1)正三角形を6つの正三角形に分けましょう
ピラミッドで考えると簡単でしょうか?実は問2を先に解いた方が簡単な気がしました。
(問2)正三角形を9つの正三角形に分けるように直線を引きましょう
9つに分ける方が、同じ大きさの正三角形でピラミッドを作ることになって、わかりやすいです。
(問2の解答例)

1,3,5と増えていく等差数列ですね。このイメージがあれば、
一番下の段が5個の正三角形なので、2段目の直線を抜けばいいや👆
と思える気がします。ということで問1の解答例は以下のようになります。
(問1の解答例)
何といっても2段目には3個の正三角形がありますから😉
例題の8つの正三角形の図がヒントというか、な~んか誘導っぽいですよね🤭
今回の「2.図形の分割」は経験的に知っていたかどうかで、差が出たかもしれません。
しかし、前回のパズル的な等分割は
(全マス目の数)÷(分けたい個数)=1個あたりのマス目の個数
という形で算数を用いた方が効率的ですし、
今回の正三角形の分割は
倍数や等差数列の概念を用いた方が、答えにたどり着きやすい
という特徴があったと思います。平面図形やパズルとは言っても、
何らかの形で算数的なものを含んでいる
と気づけたら、もっと算数が楽しくなるのだと思います。
一番楽しいのは
誰にも教えてもらわずに、自分がその法則を最初に発見した気になった時🤩
かもしれません😉
誰かに話さずにはいられない、もしかしたら大発見をしたのかも😍
というドキドキ感が、算数の魅力だと思います。美しい法則は人を惹きつけますよね。
そういう点では上の子(男子)の方が、
オレすごいの法則😤
みたいな発見は、よく報告しにきてくれた気がしました🤣
娘は
大発見🤩
の報告はあまりしてこないかもしれません🤔そのうちしてくるかも?😏
4月のマンスリー講座もボリュームはありましたが、
先生の解説が少なめだったので?若干消化不良かな~という心配はあります😓
とりあえず私ができる範囲で、娘と楽しく復習できたらいいなと思いました😉👋