4回に分けて分析と復習の様子をまとめてきたマンスリー講座2年生10月。
今回が最終回で、積み木問題の残りを書いてまいります。
(前回までの記事はこちら)
girl.chugakujuken-challenge.work
(4)積み木問題その2
さてもう一つの積み木問題は、
積み上げられた立方体の表面に見える面の数を答えよう(但し床と接する底面も数えること)
というものでした。
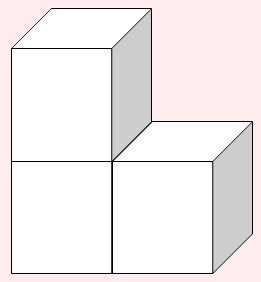
たとえば上の3個L字なら、前後左右+上下で14面(14マス)
といった感じです。つまり投影図のように見て、立方体の面のマス目で数えるということです。
(こんな風に見る)
マンスリーの出題は「平成19年・芦屋学園中の問題を少し改造したもの」でした。
(こんな感じで積み上げられていて、実際は4段まである)
授業中に面をすべて数えようとした子が居たらしく、先生から
おーい、マンスリー講座の生徒だったら数えて答え出しちゃダメだぞ~😂
と指摘があったそうです。
娘は
掛け算で出すんだよね?
というので、
どうやって掛け算にするの?
と言ったら
・・・・
ニヤッとして固まってしまったので🤣ヒントを出しました。
君きみ、これはあなたの得意なシンクシンクの「シャドーライト」ですよ
と。
シンクシンクの「シャドーライト」
すぐにピンときたようです。
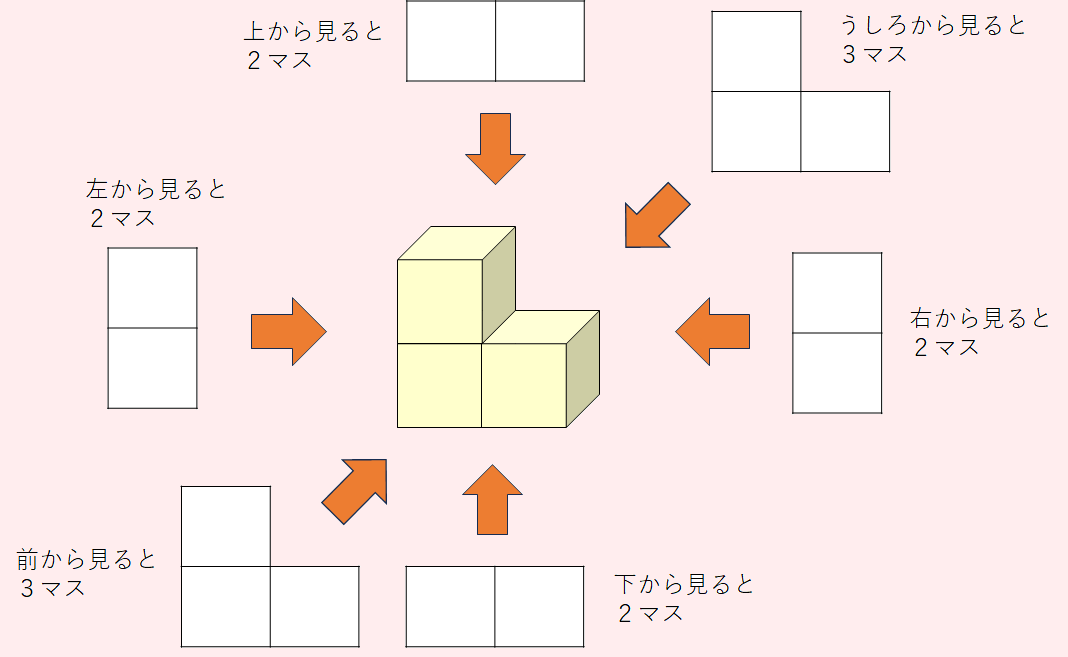
投影図で立方体のマス目を数えれば、上から1・2・3・4なので、すぐに10とわかります。
ここからは即答してほしいところでしたが、
表から見える面の数(底面含む)
が、パッとわからなかったようなので、
立方体は何面かな~?
と尋ねて「6面」を誘導しました。つまり6(面)x10(個)=60面、です。
なぜ6面なのかを教えるため
前後左右+上下だよ~
と教えましたが、とりあえず今は暗記で6面と思ってもらうことにしました。
なぜかというと
6面っていうけど、もしこれがもっと面の多い立体だったら足りないよ?👧
と疑問を投げかけてきたからです(ひえ~😅)
我々の住む空間が3次元世界であること
3次元はタテ・ヨコ・高さ(またはXYZ)
それぞれの次元で、タテなら手前・奥、ヨコなら左・右、高さなら上・下の方向がある
物体はすべて3次元構成で、見方は両極(+と-)がある
と伝えたいところですが、今じゃないかなと思いました。
レゴランドにでも連れて行って、遠くから滑らかに見えるオブジェクトが近くで見ると
立方体や直方体の集合体(つまり3次元)であることを説明・・・レゴがつまらなくなる😟
物体を抽象化して性質という観点で見るのは、もう少し先にとっておこうと思います。
10月のマンスリー講座は説明も解説も少なかったので、
何を教えたいのか推測するのが少し手間だった😵
娘に何を教えるべきなのか、楽しませるにはどうしたらいいのか?を悩まされた
と思います。小学2年生が何を楽しいと感じるか考えるなんて、プロでない私には荷が重たかった😭
頑張った頑張った・・・。
いろいろな意味で恐るべしマンスリー講座!でした~👋